 Lors du dernier article de cette série, nous avons construit un multivibrateur astable au moyen d'un amplificateur opérationnel. Ce circuit produisait un signal en créneau (signal carré).
Lors du dernier article de cette série, nous avons construit un multivibrateur astable au moyen d'un amplificateur opérationnel. Ce circuit produisait un signal en créneau (signal carré).Cette fois, nous allons transformer ce signal carré en un signal triangulaire au moyen d'un circuit intégrateur. Puis, nous allons transformer le signal triangulaire en signal carré au moyen d'un circuit différentiateur (ou dérivateur).
Dans un premier temps, je vous invite à construire à nouveau, sur un breadboard, le multivibrateur de la dernière fois (seule modification: j'ai remplacé la résistance R1 de 10K par 6K8, car ça me donnait un signal triangulaire de meilleur qualité).
Sur le breadboard, ça aura l'air de ça:
À la sortie, on obtient un signal carré, comme la dernière fois (oui, je sais, mon oscilloscope n'a pas la même intensité lumineuse partout sur l'écran, c'est irritant!).Pour transformer ce signal carré en signal triangulaire, nous allons ajouter un deuxième circuit, qu'on appelle un intégrateur (puisque son signal de sortie est l'intégrale du signal d'entrée).
C'est quoi l'intégrale? C'est une fonction qui décrit l'aire sous une courbe. Voici notre signal d'entrée:
Je divise l'aire délimitée par ce signal en petits carrés identiques entre eux:
Au temps 0, je n'ai encore traversé aucun petit carré: l'aire est nulle.
Au temps 1, j'ai traversé 2 petits carrés: l'aire est de 2 petits carrés.
Au temps 2, j'ai traversé 2 autres petits carrés, pour une aire totale de 4 petits carrés.
Au temps 3, j'ai traversé 2 carrés négatifs, qui sont soustraits de l'aire totale: donc 2 carrés.
Au temps 4, je soustrait 2 carrés supplémentaires: l'aire est redevenue nulle.
Au temps 5, je soustrait encore 2 carrés: l'aire est de -2.
Au temps 6, je soustrait 2 autres carrés: l'aire est de -4.
Au temps 7, j'additionne 2 carrés: l'aire est de -2.
Au temps 8, j'additionne 2 carrés: l'aire est nulle
Au temps 9, j'additionne 2 carrés: l'aire est de +2.
Au temps 10, j'additionne 2 carrés: l'aire est de +4.
Si je fais un graphique de l'aire en fonction du temps, ça va donc donner ceci:
Qu'est -ce que je vous disais? Un signal triangulaire!
Ça, c'est en théorie. En pratique, voici le circuit intégrateur que je vous invite à construire. Acheminez le signal de sortie du multivibrateur à l'entrée inverseuse du circuit intégrateur.
Notre breadboard se complexifie un peu:
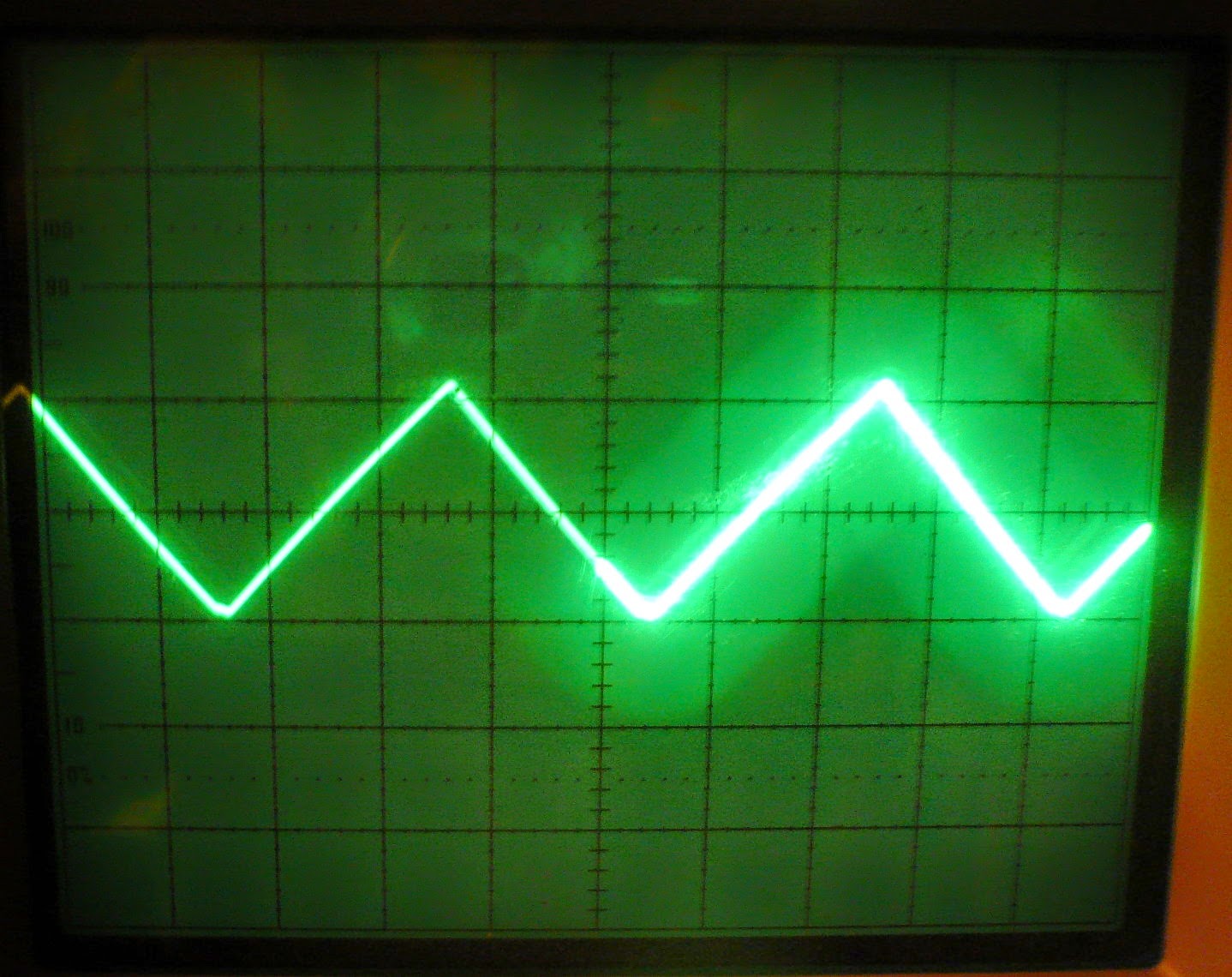
...et voilà ce que nous obtenons à la sortie de ce circuit: un signal de forme triangulaire, tel que prévu.
Amusons-nous maintenant à dériver ce signal triangulaire. La dérivée, c'est la pente de notre fonction: notre signal triangulaire a une pente positive, puis négative, puis positive, puis négative.
La dérivée est le contraire de l'intégrale: si on intègre un signal carré, ça donne un signal triangulaire, et si on dérive un signal triangulaire, ça donne un signal carré.
Voici le circuit différentiateur qui fera la dérivée de notre signal triangulaire:
Le breadboard commence à faire peur:
Et voici le résultat:
Article suivant: Amplificateurs opérationnels (5): amplificateur inverseur
Article précédent: Amplificateurs opérationnels (3): multivibrateur astable
Yves Pelletier (Twitter: @ElectroAmateur)













merci pour cette explication lumineuse de l'intégration !!!depuis le temps que je butais dessus ....
RépondreSupprimerSuper, merci mais ce qu'il manque toujours dans les explications c'est dans quel contexte c'est utile dans quel type de circuit et pourquoi c'est utile en dehors de faire un genérateur de fonctions. Quand et pourquoi c'est utile de changer un signal carré en triangle et inversement...
RépondreSupprimer🙏🙏🙏 mrc beaucoup
RépondreSupprimer